-
Privacywetgeving
Het is bij Helpmij.nl niet toegestaan om persoonsgegevens in een voorbeeld te plaatsen. Alle voorbeelden die persoonsgegevens bevatten zullen zonder opgaaf van reden verwijderd worden. In de vraag zal specifiek vermeld moeten worden dat het om fictieve namen gaat.
Opgelost Zomaar een meetkundig probleem.
- Onderwerp starter jverkerk
- Startdatum
Dit topic is als opgelost gemarkeerd
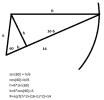
Laat een loodlijn neer vanuit het middelpunt op het lijnstuk met lengte 16. Trek ook een lijn van het middelpunt naar het snijpunt van de 16-lijn met de cirkel. Van de aldus ontstane kleine driehoek is de hoogte h=6cos(60) en de basis 6sin(60).
Van de grote driehoek is de hoogte h dus ook bekend, en de basis is dan 16 minus de basis van het kleine driehoekje.
Met Pythagoras is dan eenvoudig de straal van de cirkel te berekenen, en die is precies 14.
Van de grote driehoek is de hoogte h dus ook bekend, en de basis is dan 16 minus de basis van het kleine driehoekje.
Met Pythagoras is dan eenvoudig de straal van de cirkel te berekenen, en die is precies 14.
Warme bakkertje
Meubilair
- Lid geworden
- 13 apr 2008
- Berichten
- 7.822
- Besturingssysteem
- Windows 10
- Office versie
- Office 2021 Prof Plus EN
Johan,
De rechtse afbeelding lijkt mij de Wet van Cosines dus veronderstel ik dat deze vrij accuraat is.
De rechtse afbeelding lijkt mij de Wet van Cosines dus veronderstel ik dat deze vrij accuraat is.
whittey
Terugkerende gebruiker
- Lid geworden
- 11 mrt 2005
- Berichten
- 3.723
Je kunt deze oplossen met de stelling van Pythagoras ..
16kwadraat +6kwadraat en dan de wortel van de som,
De som is in dit geval 256+36=292, en van die 292 neem je de wortel, en kom je op het antwoord van 17,088 welke dus de straal is.
Ik vraag me bij deze af hoe een straal vierkante meter genoemd kan worden .. (zie derde regel in getypt antwoord)
16kwadraat +6kwadraat en dan de wortel van de som,
De som is in dit geval 256+36=292, en van die 292 neem je de wortel, en kom je op het antwoord van 17,088 welke dus de straal is.
Ik vraag me bij deze af hoe een straal vierkante meter genoemd kan worden .. (zie derde regel in getypt antwoord)
Laatst bewerkt:
whittey
Terugkerende gebruiker
- Lid geworden
- 11 mrt 2005
- Berichten
- 3.723
Jullie hebben gelijk, @AHulpje en @emields Ik heb de formule foutief toegepast, het moet zijn : De wortel van 16kwadraat minus 6kwadraat, en dan kom ik op 14,83 uit.
De haakse hoek haal ik uit het gegeven dat : De punt aan het einde van de 6 units lijn is een indicator voor het midden van de cirkel. De tegenover liggende hoek is 60 graden, daarbij komt dan dat de scherpehoek 30 graden is, en we weten dat een 3hoek een totaal heeft van 180 graden, minus de 30 en 60 graden hoek, dan houdt je 90 graden over, een (rechte) haakse hoek ! (en kan Pythagoras toegepast worden)
De haakse hoek haal ik uit het gegeven dat : De punt aan het einde van de 6 units lijn is een indicator voor het midden van de cirkel. De tegenover liggende hoek is 60 graden, daarbij komt dan dat de scherpehoek 30 graden is, en we weten dat een 3hoek een totaal heeft van 180 graden, minus de 30 en 60 graden hoek, dan houdt je 90 graden over, een (rechte) haakse hoek ! (en kan Pythagoras toegepast worden)
whittey
Terugkerende gebruiker
- Lid geworden
- 11 mrt 2005
- Berichten
- 3.723
